Реализация фильтров на операционных усилителях

С ростом порядка фильтра его фильтрующие свойства улучшаются. На одном ОУ достаточно просто реализуется фильтр второго порядка. Для реализации фильтров нижних частот, высших частот и полосовых фильтров широкое применение нашла схема фильтра второго порядка Саллена-Ки. На рис. 17 приведен ее вариант для ФНЧ. Отрицательная обратная связь, сформированная с помощью делителя напряжения R₃, (a – 1)R₃, обеспечивает коэффициент усиления, равный a. Положительная обратная связь обусловлена наличием конденсатора С₂. Передаточная функция фильтра имеет вид:

.

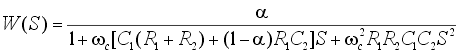(21)

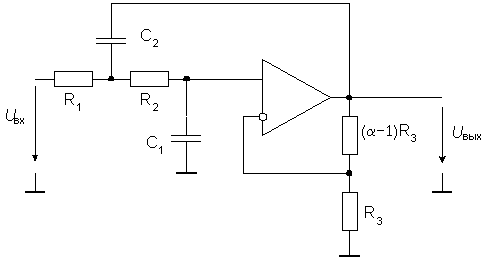
Рис.17. Активный фильтр нижних частот второго порядка

Расчет схемы существенно упрощается, если с самого начала задать некоторые дополнительные условия. Можно выбрать коэффициент усиления a = 1. Тогда (a – 1)R₃ = 0, и резистивный делитель напряжения в цепи отрицательной обратной связи можно исключить. ОУ оказывается включенным по схеме неинвертирующего повторителя. В простейшем случае он может быть даже заменен эмиттерным повторителем на составном транзисторе. При a = 1 передаточная функция фильтра принимает вид:

.

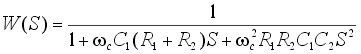Считая, что емкости конденсаторов С₁ и С₂ выбраны, получим для заданных значений а₁ и b₁ (см. (13)):

K₀ = 1,

.

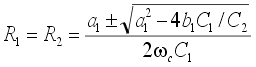Чтобы значения R₁ и R₂ были действительными, должно выполняться условие

.

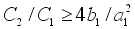Расчеты можно упростить, положив R₁ = R₂ = R и С₁ = С₂ = С. В этом случае для реализации фильтров различного типа необходимо изменять значение коэффициента a. Передаточная функция фильтра будет иметь вид

.

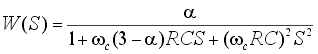Отсюда с учетом формулы (13) получим

,

.

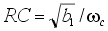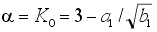Из последнего соотношения видно, что коэффициент a определяет добротность полюсов и не влияет на частоту среза. Величина a в этом случае определяет тип фильтра.

Поменяв местами сопротивления и конденсаторы получим фильтр верхних частот (рис. 18). Его передаточная функция имеет вид:

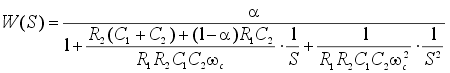
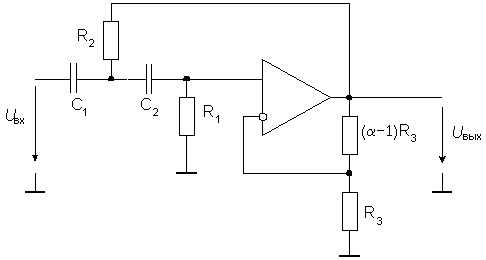
Рис. 18. Активный фильтр верхних частот второго порядка

Для упрощения расчетов положим a = 1 и С₁ = С₂ =С. При этом получим следующие формулы:

K_беск = 1, R₁ = 2/w_cCa₁, R₂ =a₁/2w_cCb₁.

Если АЧХ фильтра второго порядка оказывается недостаточно крутой, следует применять фильтр более высокого порядка. Для этого последовательно соединяют звенья, представляющие собой фильтры первого и второго порядка. В этом случае АЧХ звеньев фильтра перемножаются (в логарифмическом масштабе – складываются). Однако следует иметь в виду, что последовательное соединение, например, двух фильтров Баттерворта второго порядка, не приведет к получению фильтра Баттерворта четвертого порядка. Результирующий фильтр будет иметь другую частоту среза и другую частотную характеристику. Поэтому необходимо задавать такие коэффициенты звеньев фильтра, чтобы результат перемножения их частотных характеристик соответствовал желаемому типу фильтра.

Полосовой фильтр второго порядка можно реализовать на основе схемы Саллена-Ки, как это показано на рис. 19. Передаточная функция фильтра имеет вид:

.

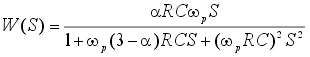(22)

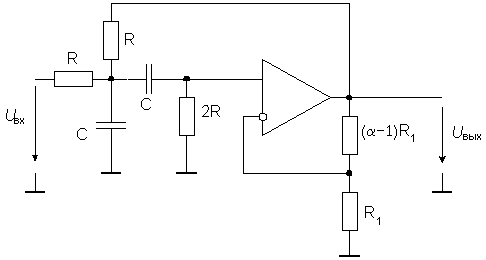
Рис. 19. Схема полосового фильтра второго порядка

Приравнивая коэффициенты этого выражения к коэффициентам передаточной функции (18), получим формулы для расчета параметров фильтра:

f_p = 1/2pRC; K_p = a/(3 – a); Q = 1/(3 – a).

Недостаток схемы состоит в том, что коэффициент усиления на резонансной частоте K_p и добротность Q не являются независимыми друг от друга. Достоинство схемы – ее добротность изменяется в зависимости от a, тогда как резонансная частота от коэффициента a не зависит.

Активный заграждающий фильтр может быть реализован на основе двойного Т-образного моста. Хотя двойной Т-образный мост сам по себе является заграждающим фильтром, его добротность составляет только 0,25. Ее можно повысить, если мост включить в цепь обратной связи ОУ. Один из вариантов такой схемы приведен на рис. 20. Сигналы высоких и низких частот проходят через двойной Т-образный мост без изменения. Для них выходное напряжение фильтра равно aU_вх. На резонансной частоте выходное напряжение равно нулю. Передаточная функция схемы на рис. 20 имеет вид:

,

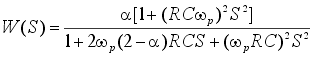или учитывая, что w_р= 1/RC,

.

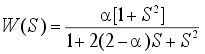(23)

С помощью этого выражения можно непосредственно определять требуемые параметры фильтра. Задав коэффициент усиления неинвертирующего усилителя равным 1, получим Q=0,5. При увеличении коэффициента усиления добротность растет и стремится к бесконечности, если a стремиться к 2.

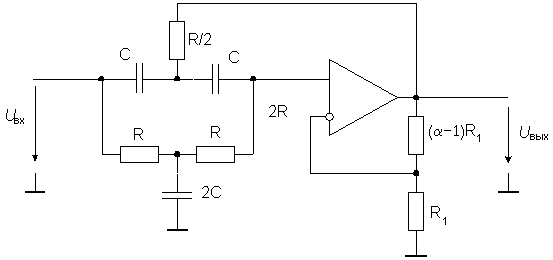
Рис. 20. Активный заграждающий фильтр с двойным Т-образным мостом