Схема дифференцирования

Поменяв местами резистор и конденсатор в схеме интегратора на рис. 2, получим дифференциатор (рис. 5). Применение первого закона Кирхгофа для инвертирующего входа ОУ в этом случае дает следующее соотношение:

C(dU_вх/dt) + U_вых/R = 0,

или

U_вых = – RC(dU_вх/dt).

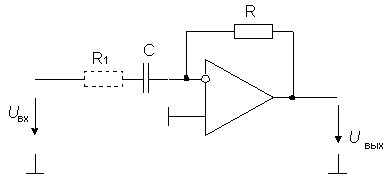
Рис. 5. Схема дифференциатора

   Используя формулу

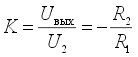
и учитывая, что в схеме на рис. 5 вместо R₁ используется 1/sC, a R₂=R, найдем передаточную функцию дифференциатора

    Подставив в (3) s=jw , получим частотную характеристику дифференциатора:

K(jw) = -jwRC,

модуль которой

пропорционален частоте.

Практическая реализация дифференцирующей схемы, показанной на рис. 5, сопряжена со значительными трудностями по следующим причинам:

• во-первых, схема имеет чисто ёмкостное входное сопротивление, которое в случае, если источником входного сигнала является другой операционный усилитель, может вызвать его неустойчивость;

• во-вторых, дифференцирование в области высоких частот, в соответствии с выражением (4), приводит к значительному усилению составляющих высоких частот, что ухудшает соотношение сигнал/шум;

• в-третьих, в этой схеме в петле обратной связи ОУ оказывается включенным инерционное звено первого порядка, создающее в области высоких частот запаздывание по фазе до 90°:

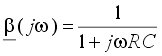
Оно суммируется с фазовым запаздыванием операционного усилителя, которое может составлять или даже превышать 90°, в результате чего схема становится неустойчивой.

Устранить эти недостатки позволяет включение последовательно с конденсатором дополнительного резистора R₁ (на рис. 5 показан пунктиром). Следует отметить, что введение такой коррекции практически не уменьшает диапазона рабочих частот схемы дифференцирования, т.к. на высоких частотах из-за снижения усиления в цепи обратной связи она все равно работает неудовлетворительно. Величину R₁С (и, следовательно, ноль передаточной функции RС – цепи) целесообразно выбирать так, чтобы на частоте f₁ усиление петли обратной связи составляло 1 (см. рис. 6).

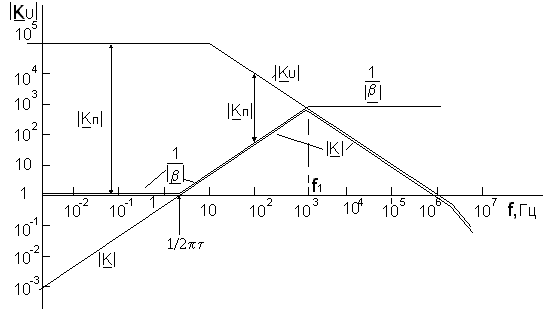
Рис. 6. ЛАЧХ схемы дифференцирования на ОУ